백준 7562 나이트의 이동

www.acmicpc.net/problem/7562

7562번: 나이트의 이동

---

 이 문제를 처음 보면 어떻게 풀어야 할 지 감이 안 잡힌다. 그러나 잘 생각해보면 BFS를 이용해서 풀 수 있는 문제라는걸 알 수 있다.

나이트가 이동할 수 있는 방향은 왼쪽과 같다. 문제는 이렇게 이동할 수 있는 나이트를 시작위치에서 종료위치로 옮기는 최소횟수를 구하는 것이다.

 차례대로 생각을 해보자면, 나이트는 시작위치에서도 저 8개 위치로만 이동할 수 있고, 8개 위치 중 하나를 골라 이동한 뒤에 또 8개 위치 중 하나로 이동할 것이다. 그렇게 해서 목적지에 도착하는 순간이 있을 것이다. 이것을 트리로 바꿔보면 아래와 같다.

 

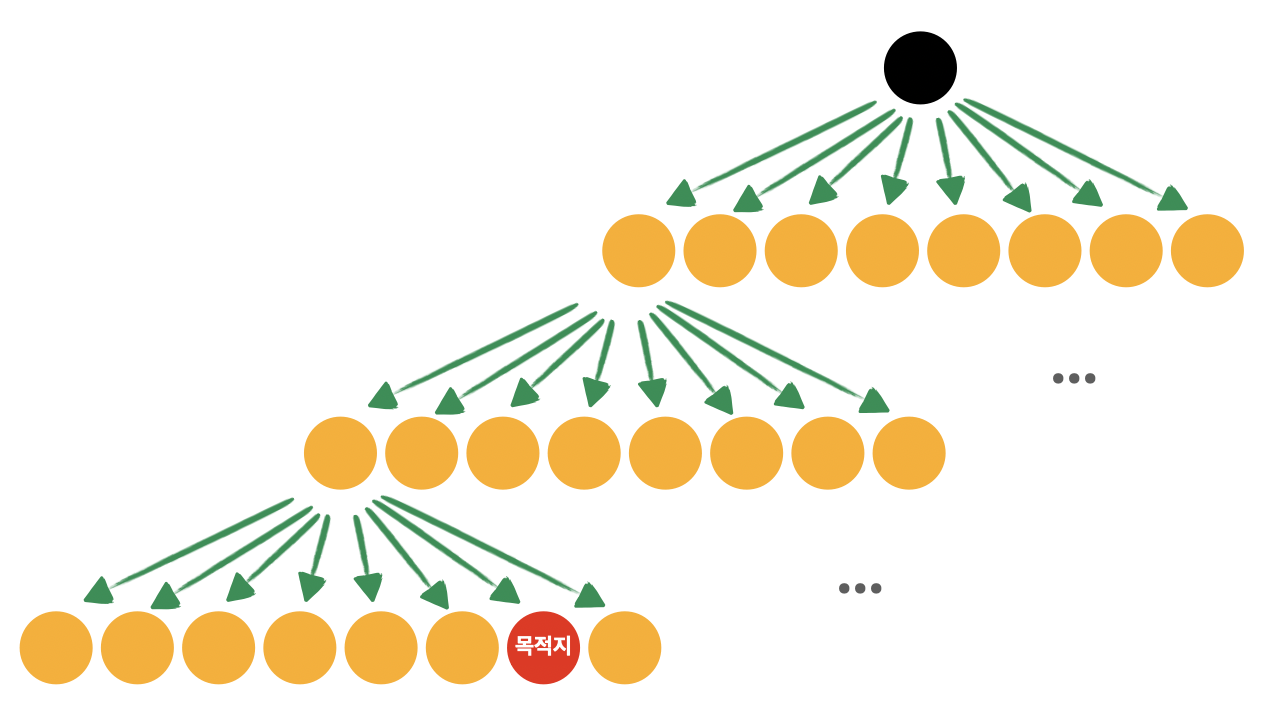
 검은 점이 시작점이고, 빨간 점이 시작점이다. 결국 트리를 탐색하는 방법을 사용하면 목적지에 도착하는 최소횟수를 구할 수 있다.

 이때, DFS가 아니라 BFS로 구해야 하는 이유는 (내 생각엔) DFS로 구하게 되면 하나의 노드를 잡고 그 끝까지 갔다가 만약에 없다면 다시 횟수를 초기화해야하는데 그 처리가 상대적으로 어렵기 때문인 것 같다. 어떤 분께서 이 문제의 경우는 최소횟수를 구해야 하는 문제이므로 DFS로 구하게 되면 제일 아래의 깊이까지 들어가기 때문에 BFS로 구하는 것이 맞다고 알려주셨다. BFS로 구할 때는 첫번째 단계를 전부 탐색하고 두번째 단계로 넘어가기 때문에 횟수를 초기화해주지 않아도 편리하게 구할 수 있다.

def bfs(now_x, now_y, final_x, final_y):

    q=deque()

    # 시작점을 지나온 것으로 처리한다.
    q.append((now_x, now_y))
    board[now_x][now_y]=1

    while q:
        x, y=q.popleft() # 좌표를 꺼내서
        if x==final_x and y==final_y: # 목적지에 도착
            print(board[final_x][final_y]-1)
            return
        # 목적지가 아닌 곳이면
        for i in range(8): # 8개 방향 탐색
            nx, ny=x+dx[i], y+dy[i]
            if 0<=nx<board_length and 0<=ny<board_length and board[nx][ny]==0: # 새로운 위치가 이동할 수 있는 위치이면 그 위치로 이동
                q.append((nx, ny))
                board[nx][ny]=board[x][y]+1